Details of the calculation
We are striving to express, for a given type of insulin, the percentage of the
hypoglycemic power, function of the dosage and the time elapsed since the injection.
Let's consider the minimal Um and maximal UM number of insulin units
the diabetic can inject.
Let p be the hypoglycemic power at t0 and t2
times.
Let M and m the maximal and minimal percentages of the hypoglycemic
power at time t1, corresponding respectively to a dosage of
Um and UM units of insulin.
At last, D (m ≤ D ≤ M) denotes the percentage of the hypoglycemic
power at time t1, corresponding to a dosage of
U units of insulin (Um ≤ U ≤ UM).
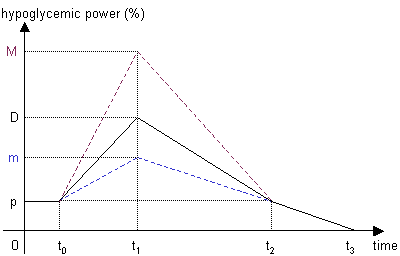
Then the expression of the hypoglycemic power at time t is, function of D:
|
HPt =
|
p |
if t ≤ t0 |
|
|
if t0 < t < t1
|
| D(t - t0) - p(t - t1) |
| t - t1 |
|
if t1 < t < t2
|
| p(t - t1) - D(t - t2) |
| t3 - t2 |
|
if t2 < t < t3
|
|
0
|
if t ≥ t3
|
We have now to find the expression of D. So we have the equation (1):
| M - m |
= |
D* |
with D = D* + m. |
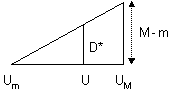 |
| UM - Um |
U - Um |
In our experiment, we have m = 30% and M = 100%.
With the regular insulin, the minimal number of units is Um = 1
and the maximum numner is UM = 9.
By substitution in equation (1), we obtain:
| 100 - 30 |
= |
D* |
| 6 - 1 |
U - 1 |
| so D* = |
70 |
(U - 1) = 14U - 14 |
| 5 |
| With D = D* + m = 14U - 14 + 30, we have | Dregular = 14U + 16 |
Concerning lente insulin, Um = 9 and UM = 12. So:
Finally:
| D = D* + 30 = |
70 |
(U - 9) + 30 |
= |
70 |
U - 210 + 30 |
| 3 |
3 |

